17:0と1だけの世界
それで、ロンリーエンジンってなんだよ?ちょっとかっこいい言葉だが、おまえもジジイも顔が引きつってたし、どうも気になるぜ。
論理演算だよ。そうだね・・・いよいよ試練に立ち向かう時が来たかもしれないね。
よせよおどかしやがって、失敗したら死ぬようなシレンじゃねえだろうな。
ハハハ、死ぬ事はないよ。論理演算ってのは、プログラミングで避けて通れない考え方なんだけど、結構難しいんだよ。それでここまでは論理演算をわざと避けてきたんだけど、先に進むにはそろそろ基本を理解してもらわないとダメかもね。
おいおい、見た事もないややこしい数式とか出てくるんじゃねえだろうなあ・・・
いや、数学は数学でも、数式はほとんどいらないんだ。数字も0と1だけしか使わないよ。
なんだよ、0と1しか使わないならもうオレサマの勝利は決まったも同然じゃないか!
本当に大丈夫かなあ。
0と1だけなんだけど・・・いや、グズグズ言ってても仕方がない。じゃあいくよ!
ねえ、コンピューターってものすごい速さでものすごい計算をいっぱいしてくれるけど、数は0からいくつまで知っていると思う?
そりゃあ、すげえいっぱいまで知ってるんじゃねえのか?100億とか1000兆とかよ。
実はコンピューターは0と1しか知らないんだ。
な、なにぃ・・・やいインテリ、いいかげんなこと言ってんじゃねえぞ。0と1だけじゃ電卓にもならねえぞ。けどちゃんと電卓になったじゃねえか!
1個の0と1だけじゃあ何にもできないね。コンピューターはね、0と1をたくさんたばねて計算する事ができるのさ。
例えばSwitchは0か1を32個とか64個たばねたものを数として使うんだ。そうだねえ、0か1って言ってるけど、1個のライトだと思ってよ。光ってたら1、消えてたら0。そのライトが32個か64個ずらっと並んでる。想像できるかな?
それくらいなら想像つくぜ。
じゃあ32個のランプがそれぞれついたり消えたりするとして、その光り方のパターンて何個あるかわかるかい?
それぞれがついたり消えたりするんだな。一番右がついて、消えて、その隣がついてる時に一番右がついて、消えて、もうひとつ隣がついてる時に・・・うおお!数えられねえ!
ランプ1個だと2通りだよね。ついてるのと消えてるの。2個だと4通りになるのはわかるかな?、じつは3個だと8通り、4個だと16通り・・・と、倍々に増えていくんだ。
そして32個あると、なんと42億通りの光り方があるのさ。正確には42億9496万7296通りだけどね。
そりゃあ数えられないわけだぜ。
そこで、この光り方1個1個に普通の数を振っていくと、0から42億までの数を32個のランプの光り方で表す事ができるのさ、どう?ここまでは大丈夫?
ものすげえ数だが、ようは光り方ごとに番号を振るんだな?
そう!それで、このランプの事をビットって言うよ。32個のランプは32ビットさ。そしてコンピューターはこのビットってやつを使ってなんでもかんでも計算するんだ。
ランプのオンオフ、つまり0と1の2種類の数だけ使うから、2進数っていう言い方をするんだ。言い換えるとコンピューターは2進数で計算をしているって事だね。
さて、2進数の話もすごく大事だけど、今回はここまでにして、ここからはランプ1個だけの計算を考えよう。そこで出てくるのが論理演算なんだよ。
ランプ1個ってことは光ってるか光ってないだけじゃねえか。計算もへったくれもあるのかよ。
それがあるのさ!
計算だから、ランプ1個と、もう1個のランプを考えよう、そして計算結果のランプもあるよ。
普通の計算は、足し算、引き算、かけ算、割り算の4つの計算があるよね?論理演算、つまりランプとランプの計算方法もそれと似ているよ。最初はへんてこりんに見えるけど慣れればなんてことはない。
まずAND。ランプが両方ついている時だけ、計算結果のランプもつくんだ。どっちか一方が消えてたり、両方消えてたら、計算結果ランプも消えるよ。
えーと、数字に置き換えると、1 AND 1は1で0 AND 1は0ってことかな?
そう!いいね!
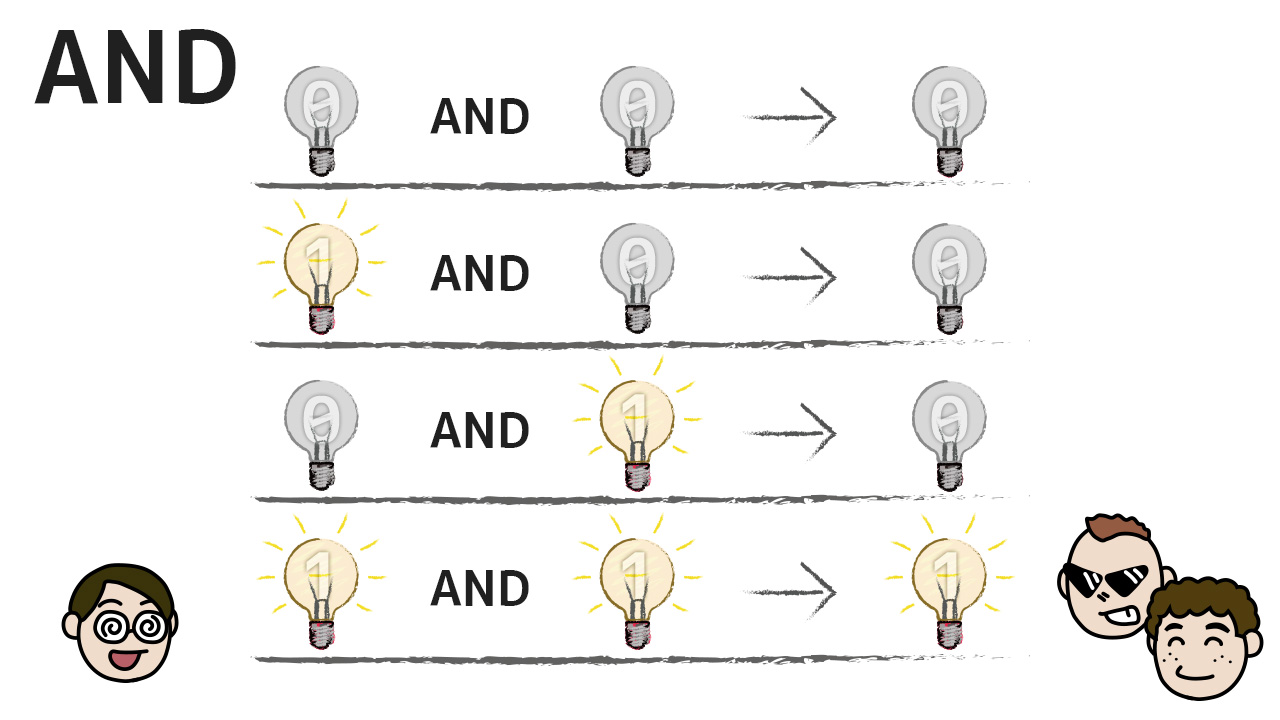
次にOR。これはランプがどちらか一方でもついていたら、計算結果ランプもつくんだ。結果ランプが消えるのは両方消えてる時だけだよ。
うう、つ、つまり、1 OR 0は1、0 OR 1も1で、0 OR 0は0、か?
そうそう!君たちはやっぱりプログラミングのセンスがあるよ!

次はNOT。これはランプ1個だけ。光り方をひっくり返す計算だよ。NOT 0が1に、NOT 1が0になるんだ。
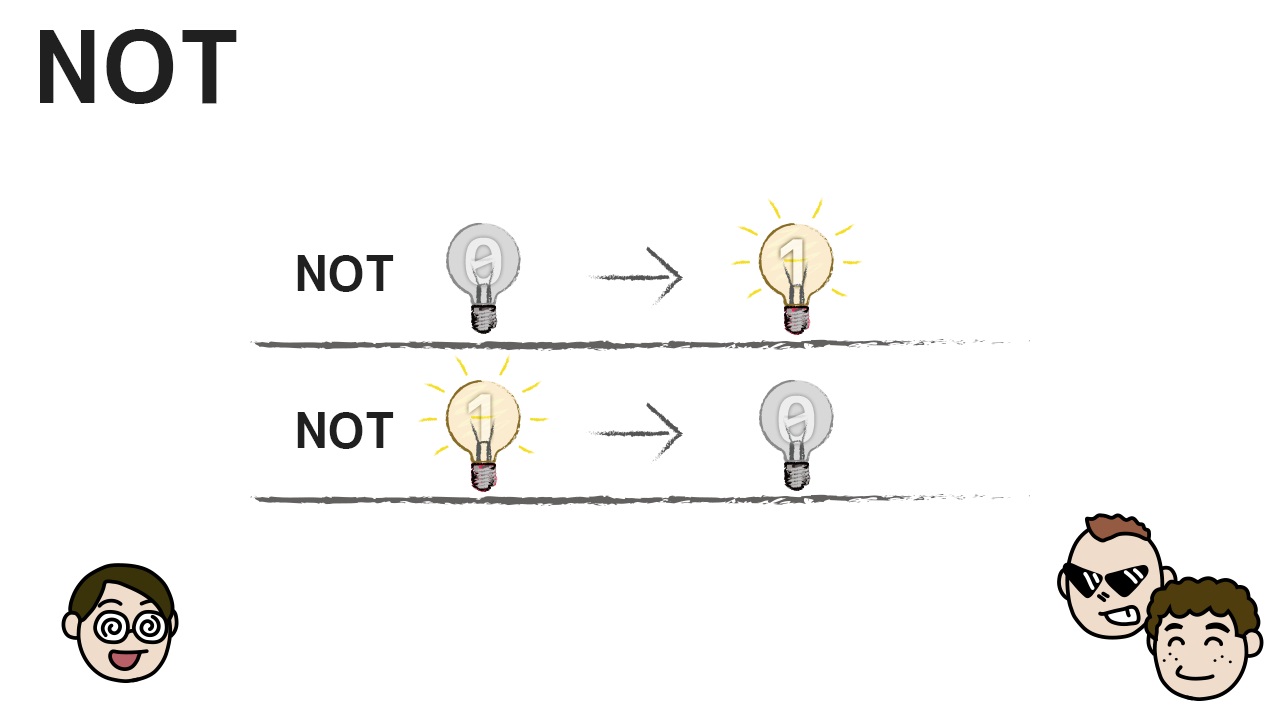
ちなみに日本語ではANDは論理積、ORは論理和、NOTは論理否定と言うよ。名前の通りANDはかけ算、ORは足し算に似てるんだ。
まとめると、ANDはビットのかけ算、ORはビットの足し算、NOTはなんだかマイナスつけるっぽい感じ?
そうだね。この3つの計算方法を組合わせるだけで、いろいろな計算ができるんだ。
ランプ1個の計算ができることはわかったぜ。0と1だけだからカンタンだしな。でも0と1だけ計算できてもなんの役にも立たねえんじゃねえのか?
ここからが本番さ。
話は飛ぶけど、IF文ってあるよね?
ハナシをごまかすんじゃねえ、IF文とランプってなんの関係もねえだろう。
ワンパク君、IF文って何をするんだったっけ?
ナニー!てめえ人の話聞いてねえのかよ!IF文なんて、正解ならTHENから先を実行する、間違ってたら実行しない、ランプと全然関係ねームキー!
それで、さっきボクが言ったこと覚えてるかな?コンピューターは全部の計算を0か1、つまりビットでやるんだよね?てことはIF文もビットでやってるんだけど、どうやると思う?
へ・・・?
あ・・・
ちょっと待てよ・・・条件が正解なら実行する、間違ってたら実行しない・・・ビットっつうかランプ・・・ついてたら実行する、消えてたら実行しない・・・!
フフ、もう少しかな?
正解だとランプがつく、間違ってるとランプが消えるとすれば、正解だとランプがついて実行する、間違ってたらランプがつかないから実行しない・・・
つまり、条件が正解かどうかでランプがついたり消えたりして、IF文はそのランプを見てTHENを実行したりしなかったりする!
正解!
ビットで言い換えると、IF文は条件の結果を、正解なら1、間違ってたら0っていうふうに解釈するんだ。そして、条件の結果が1だったら正解だと思ってTHENを実行するんだよ。
IF文の条件のところで==とか<とか書くだろう?あれは実は値が同じなら1、違ったら0だったり右の値の方が大きかったら1、そうじゃなかったら0っていう意味なんだよ。そしてその結果でTHENを実行したりしなかったりする。これがIF文の中でコンピューターが行っている事なんだよ。
IF文も0と1だけで動いてるのはわかったぜ。でもANDやORはどこ行ったんだ?
じゃあ、また話は飛ぶけど、15章の弾を撃つ時のIF文覚えてるかな?
うおーまた飛びやがって!覚えてるぜ!マリョリョ・・・
IF文の中にIF文を書いてたやつだよね?
'まずたまがないことをチェック
IF TAMA==0 THEN
'つぎにボタンをチェック
IF BUTTON(1,#B_RRIGHT)==1 THEN
'たまはっしゃ!
ENDIF
ENDIF
これこれ。
これ、実はIF文1個で書けるんだ。
リョリョ・・・へ?
日本語でこのコードを説明すると弾がなくて、ボタンが押されていたら、弾発射だよね?
これをランプに置き換えてみよう。ボタンが押されたらランプが付く、弾がなかったらもう1個ランプが付くって考えたら、どうなる?
ランプが2個ついたら、弾発射、かな?あれ?なんか聞いた事あるような・・・
ANDじゃねえか!ランプが2個付いたら、計算結果のランプがつく!
そう!つまり弾がない AND ボタンが押されているってこと!
これをBASICで書くとこうなるんだ!
IF TAMA==0 && BUTTON(1,#B_RRIGHT)==1 THEN
'たまはっしゃ!
ENDIF
IF文の中のANDは&&って書くよ。&&両側の結果が1だったら、つまりどっちも正解なら、THEN実行っていう事になるよ!
な、なるほど、ANDとIFがこうつながるわけか。
でもよう?IF文ふたつ組合わせれば今までだって書けたわけだよな?ANDだのORだのわざわざややこしい説明をしたってことは、変数の時と同じなにかウラがあるんだろう。
フフ、まだORの出番が来てないしね!IF文を入れ子にしただけじゃ絶対に書けない事をやってみよう。Aボタンだけじゃなく、Xボタンでも弾を発射したいと思ったらどうする?「弾がない時に」はいったんはずして、ボタンだけで考えてみて。
うう、全然わからねえ・・・
まず日本語で書いてみよう!Xボタンは#B_RUPだよ!
ええと、B_RRIGHTが押されたか、B_RUPが押されたかしたら、タマ発射か。
IF文だけで行くぜ。ええと、ええと・・・ダメだ、書けねえ・・・
このアレしたかソレしたかのどっちかっていうのに使うのがORなんだよ!
B_RRIGHTが押された OR B_RUPが押されたってことか?
正解!じゃあそこに弾がないってのを付け足してみようか。
さっきのANDをくっつけりゃいいんだろう?タマがない AND B_RRIGHTが押された OR B_RUPが押されただな。
おしい!OR と ANDが両方出てきた時は、ANDが先に計算されるんだ。足し算とかけ算が混ざっていたらかけ算を先にやるのと同じだね。そういうときに足し算を先にやる方法は算数でならったはず!
かっこか!タマがない AND (B_RRIGHTが押された OR B_RUPが押された)ってことだな!
正解!
プチコンを始める前はかっこなんて使えなかったのにね。
神崎、そろそろオレのイエローカードが出てくるぞ。
じゃあそのままプログラムにしてみてよ!IF文の中ではORは||って書くよ!
よし・・・
IF TAMA==0 && (BUTTON(1,#B_RRIGHT)==1 || BUTTON(1,#B_RUP)==1) THEN
'たまはっしゃ!
ENDIF
こうか!
正解!
まとめるよ。論理演算を使うと、IF文の条件をいくつも組合わせて複雑な条件にできるんだ。AND、IF文の中だと&&だね、これはふたつの条件が両方正解だったら、ORは||、これはふたつの条件のどちらか、もしくは両方正解だったら、NOTは今回出てこなかったけどIF文では!と書いて、使うと正解不正解をひっくり返せるよ。
&&、||、!の読み方は人によってまちまちだけど、ボクはそれぞれアンドアンド、オアオア、ノットって読んでるね。!は正式にはエクスクラメーションマークって言うんだけどプログラムの中でちゃんとそう読む人は少ないんじゃないかな。あ、ハカセはビックリって読んでたよ。
そして大事なのは、IF文の条件が正解かどうかってのも、コンピューターの中ではビットが0か1かっていう事で計算してるって事さ。複雑な条件を書いた時も、それぞれの条件が0か1かに置き換わって、そしてその間でAND,OR,NOTなんてのを使って、最終的に0か1かになるっていう事だよ。
この物事を0か1かのビットのカタマリで扱うというのを、デジタル処理と言うぞい!今のコンピューターはあらゆる事を0か1かのデジタルデータとして処理するから、デジタルコンピューターと言うんじゃ!
余談になるが、全部0か1じゃなくて、0.5とか1.33とかもあっていいんじゃない?という処理の仕方はアナログ処理と言うんじゃ。そしてなんとアナログコンピューターというのもあるんじゃよ。超ウルトラレアキャラじゃがのう。わしも実物を見たことがない!
さて、デジタル、つまり物事を0か1のカタマリで処理すると何が良いのかというと、ビットの計算の基本は、論理演算なんじゃ。足し算、かけ算、割り算なんてのも、実は論理演算を組合わせて行えるんじゃ。たった3つのカンタンな計算を組合わせるだけで、ありとあらゆる計算ができるというのがデジタルのすごいところなんじゃよ。
実はコンピューターの中には、ものすごい小さいランプがものすごくたくさん、何億個何十億個と入っていて、そしてそのランプを論理演算で計算する仕組みもものすごくたくさん、何億個何十億個と入っていると思えばええ!まあ実際のコンピュータに組み込まれている「ランプ」は光らんがのう。
ランプのかわりに電気が貯まっていたら1、電気がなかったら0、という事にして、あらゆる事を電気のある・なしに置き換えて計算しとるんじゃ!ある・なしだけのデジタルで計算する方が、ちょっとだけあるとか、すごくたくさんあるとかのアナログで計算するよりずっとラクなんで、世の中のほとんどのコンピューターはデジタルコンピューターになったんじゃよ。
そしてその論理演算のチカラをほんのちょっと借りて、今回はIF文なんかでややこしい条件を書けるという事を学んだわけじゃ。
それで、論理演算の基本は計算方法が3種類しかないカンタンな物なんじゃが、実際にややこしい条件をこの3つの計算の組合わせに置き換えるというのが、最大の難関なんじゃよ。そこはいろいろなパターンや法則を覚えて、経験値を少しずつ上げていくしかない!まあいつも言っとるとおり、あせらず少しずつ覚えていけばええぞい。
{今回:こんかい}のポイント
ビットについて
Switchはもちろん、今世の中にあるスマートフォン、タブレット、パソコン等のコンピューターはほとんどすべてデジタルコンピューターです。デジタルとは、データをすべて0か1のビットのかたまりとして扱う事を意味します。Switchの中のコンピューターはビットを32個、または64個のかたまりで取り扱います。
論理演算
コンピューターの中ではデジタルデータの計算をAND,OR,NOTのたった3種類の論理演算の複雑な組合わせで行っています。AND,OR,NOTそれぞれの計算内容は本編の挿絵を見て下さい。ANDはビットのかけ算、ORはビットの足し算、NOTはビットをひっくり返す計算だと思うと理解しやすいです。
{条件式:じょうけんしき}での{論理:ろんり}{演算:えんざん}
IF文などで条件式を書く場合に論理演算を使って複雑な条件を書く事ができます。ANDは&&、ORは||、NOTは!を使用します。かっこも使用できます。
式の中で&&,||,!を使わずにAND,OR,NOTと書く事もできますが、そうすると式が違う意味になるので注意してください。SmileBASICの中でAND,OR,NOTと書いた時に何が起こるかは別の章で説明します。
式の中で&&,||,!を使わずにAND,OR,NOTと書く事もできますが、そうすると式が違う意味になるので注意してください。SmileBASICの中でAND,OR,NOTと書いた時に何が起こるかは別の章で説明します。
さて、論理演算に少し慣れてもらうために、練習問題を出しておこうかの!
その1:PRINT文があるじゃろ?あれで論理演算の結果もチェックする事ができるんじゃ。たとえば? 1 && 0とやれば1 AND 0の計算結果が出てくるし、? 1 || 1とやれば1 OR 1の計算結果も出てくる。NOTも同じじゃ。? !1とやったら何が出てくるか実際に確認してくれい!そうそう、? A==0とか書いて、IF文の条件が正解かどうか簡単に確認できるぞい。覚えておくとIF文のデバッグに便利じゃ。
その2:簡単なプログラムを作ってくれい!0から9までの数の間で、3以上5以下の数だけPRINT文で出力するんじゃ。0から9までというのはFOR文を使ってFOR I=0 TO 9とかやればいけそうじゃのう。後はIF文とPRINT文じゃ。FOR文の変数がIなら、3以上はI>=3、5以下はI<=5と書けるな。ふたつの条件が同時に正解かどうか調べる方法は今回やったのう!3 4 5の3つの数が出てくれば正解じゃ!
その3:前の問題の逆パターンも作ってみようかの。0から9までの数の間で、3より下または5より上の数だけPRINT文で出すんじゃ。3より下はI<3、5より上はI>5じゃ。後はわかるな?0 1 2 6 7 8 9と7個の数が出てくれば正解じゃ!
その4:その2とその3ができた人向けの上級問題じゃ!実はその3じゃが、その2のプログラムに3文字足すだけでできるんじゃ!足す文字は!,(,)じゃ。どうすればいいじゃろうな?ヒントはその3の説明の最初、その3は1その2の逆バターンじゃ。条件の正解不正解をひっくり返す方法があったじゃろう?